Uncertainty propagation of material properties of a cantilevered beam¶
Overview¶
This is an uncertainty propagation problem modeling the effect of uncertain material parameters on the displacement of an Euler-Bernoulli beam with a prescribed load.
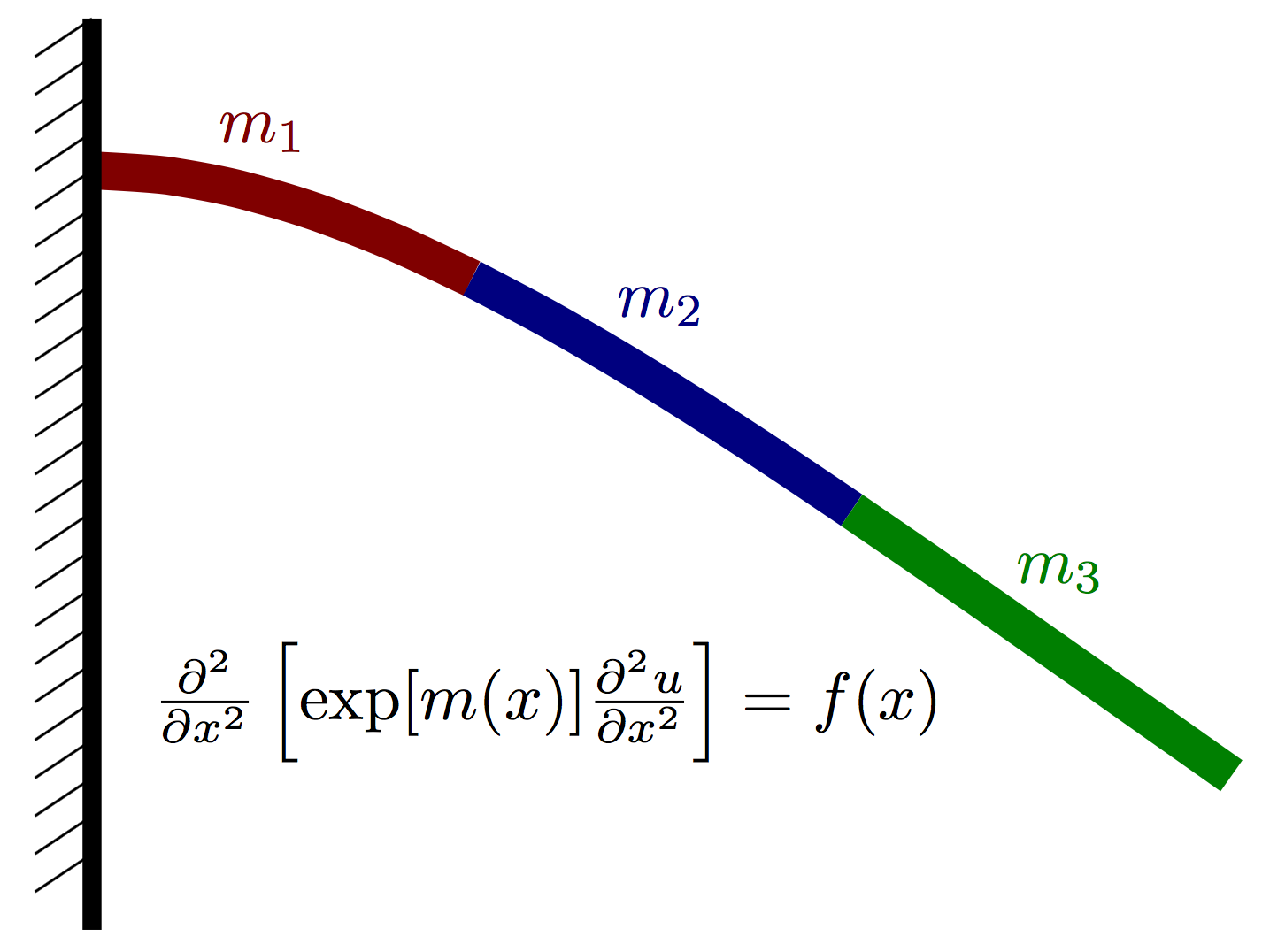
The Young’s modulus is piecewise constant over three regions as shown below, and the three constants are assumed to each be uncertain with a uniform distribution.
Run¶
docker run -it -p 4243:4243 linusseelinger/benchmark-muq-beam-propagation:latest
Properties¶
Model |
Description |
|---|---|
forward |
Forward model |
forward¶
Mapping |
Dimensions |
Description |
|---|---|---|
input |
[3] |
The value of the beam stiffness in each lumped region. |
output |
[31] |
The resulting beam displacement at 31 equidistant grid nodes. |
Feature |
Supported |
|---|---|
Evaluate |
True |
Gradient |
True |
ApplyJacobian |
True |
ApplyHessian |
True |
Config |
Type |
Default |
Description |
|---|---|---|---|
None |
Mount directories¶
Mount directory |
Purpose |
|---|---|
None |
Source code¶
Description¶
Forward model¶
Let \(u(x)\) denote the vertical deflection of the beam and let \(m(x)\) denote the vertial force acting on the beam at point \(x\) (positive for upwards, negative for downwards). We assume that the displacement can be well approximated using Euler-Bernoulli beam theory and thus satisfies the PDE
where \(m(x) = \log E(x)\) is the log of an effective stiffness \(E(x)\) that depends both on the beam geometry and material properties.
For a beam of length \(L\), the cantilever boundary conditions take the form
and
Discretizing this PDE with finite differences (or finite elements, etc…), we obtain a linear system of the form
where \(\hat{u}\in\mathbb{R}^N\) and \(\hat{f}\in\mathbb{R}^N\) are vectors containing approximations of \(u(x)\) and \(m(x)\) at finite difference nodes.
We assume that \(m(x)\) is piecwise constant over \(P\) nonoverlapping intervals on \([0,L]\). More precisely,
where \(I(\cdot)\) is an indicator function.
As our forward model, we define \( F : \mathbb{R}^3 \rightarrow \mathbb{R}^N \) mapping a parameter vector \(m = [m_1, m_2, m_3]\) onto the corresponding solution vector \(\hat{u}\).
Finally, the quantity of interest \( Q : \mathbb{R}^N \rightarrow \mathbb{R}^2 \) simply picks the solution at the 10th and 25th node, i.e. \( Q(\hat{u}) := \left(\begin{matrix} \hat{u}_{10} \\ \hat{u}_{25} \end{matrix} \right) \).
The container implements the mapping \(F\); implementing \(Q\), i.e. picking out the respective solution entries, is up to the user.
Uncertainty propagation¶
For the prior, we assume the material parameter to be a uniformly distributed random variable
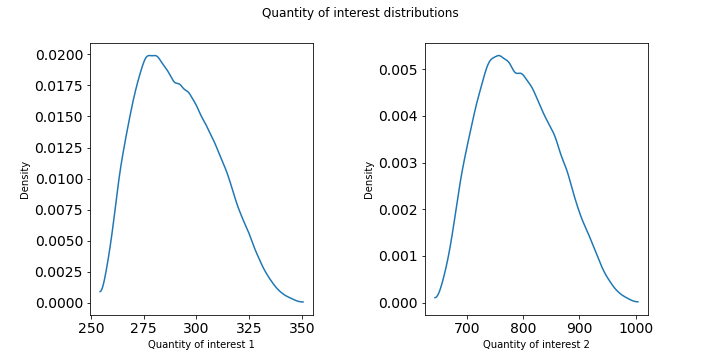
The goal is to identify the distribution of the resulting quantity of interest \(Q(F(M))\). Samples from the model output \(F(M)\) are illustrated in the following figure.

The quantity of interest’s components have the following distributions, as computed from \(10^5\) simple Monte Carlo samples.