The cookies problem forward UQ benchmark¶
Overview¶
This benchmark runs a forward uncertainty quantification problem for the cookies model using the Sparse Grids Matlab Kit interface to UM-Bridge. See below for full description.
Run¶
docker run -it -p 4242:4242 linusseelinger/cookies-problem
Properties¶
Model |
Description |
|---|---|
benchmark |
Sets the config options for the forward UQ benchmark (see below) |
Benchmark configuration¶
Mapping |
Dimensions |
Description |
|---|---|---|
input |
[8] |
These values modify the conductivity coefficient in the 8 cookies. They are i.i.d. uniform random variables in the range [-0.99, -0.2] (software does not check that inputs are within the bound) |
output |
[1] |
The integral of the solution over the central subdomain (see definition of \(\Psi\) at cookies model for info) |
Feature |
Supported |
|---|---|
Evaluate |
True |
Gradient |
False |
ApplyJacobian |
False |
ApplyHessian |
False |
Config |
Type |
Default value |
Can be changed in benchmark model |
Description |
|---|---|---|---|---|
NumThreads |
integer |
1 |
yes |
Number of physical cores to be used by the solver |
BasisDegree |
integer |
4 |
no |
Default degree of spline basis (must be a positive integer) |
Fidelity |
integer |
2 |
no |
Controls the number of mesh elements (must be a positive integer, see below for details) |
Mount directories¶
Mount directory |
Purpose |
|---|---|
None |
Source code¶
Description¶
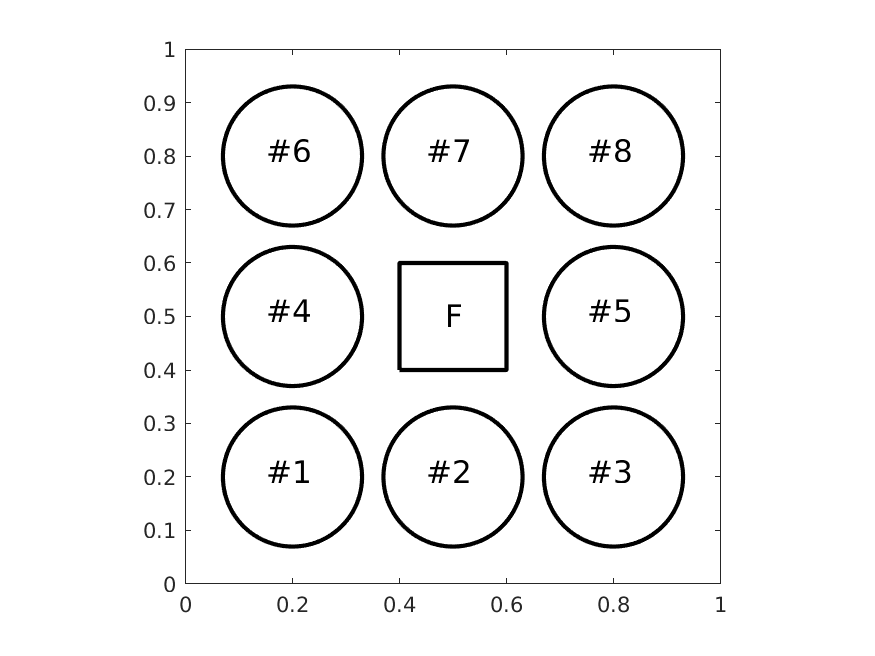
The benchmark implements a forward uncertainty quantification problem for the cookies model. More specifically, we assume that the uncertain parameters \(y_n\) appearing in the definition of the diffusion coefficient are uniform i.i.d. random variables on the range \([-0.99, -0.2]\) and we aim at computing the expected value of the quantity of interest (i.e., output of the model) \(\Psi\), which is defined as the integral of the solution over \(F\).
The PDE is solved with an IGA solver that uses as basis splines of degree \(p=4\) and maximal regularity, i.e. of continuity \(3\), and the mesh has \(200 \times 200\) elements (i.e., the fidelity config parameter is set to \(2\)). The structure of this benchmark is identical to the one discussed in [Bäck et al.,2011]; however, raw numbers are different since in [Bäck et al.,2011] the PDE solver employed was different (standard FEM with piecewise linear basis) and the mesh was also different.
As a reference value, we provide the approximation of the expected value computed with a standard Smolyak sparse grid, based on Clenshaw–Curtis points, for level \(w=5\), see e.g. [Piazzola et al.,2023]. The resulting sparse grid has 15713 points, and the corresponding approximation of the expected value is \(0.064196096847169\).
The script available here generates the results, using the Sparse Grids Matlab Kit [Piazzola et al.,2023] for generating sparse grids. The Grids Matlab Kit is available on Github here and a dedicated website with full resources including user manual is available here.