Composite material with random wrinkle

Overview

This model implements the 3D anisotropic linear elasticity equations for a composite part with randomised wrinkle. The maximum deflection of the part is estimated by embedding a wrinkle into a high fidelity FE simulation using the high performance toolbox dune-composites.

Authors

Anne Reinarz

Run

docker run -it -p 4242:4242 linusseelinger/model-dune-composites:latest

Properties

Model	Description
forward	Linear elasticity

forward

Mapping	Dimensions	Description
input	[346000]	Coefficients of a Karhunen Loeve expansion of a wrinkle.
output	[1]	Maximum deflection of the composite part.

Feature	Supported
Evaluate	True
Gradient	False
ApplyJacobian	False
ApplyHessian	False

Config	Type	Default	Description
ranks	int	2	Number of MPI ranks (i.e. parallel processes) to be used.
stack	string	“example2.csv”	Path to the stacking sequence to be run.

Mount directories

Mount directory	Purpose
None

Source code

Model sources here.

Description

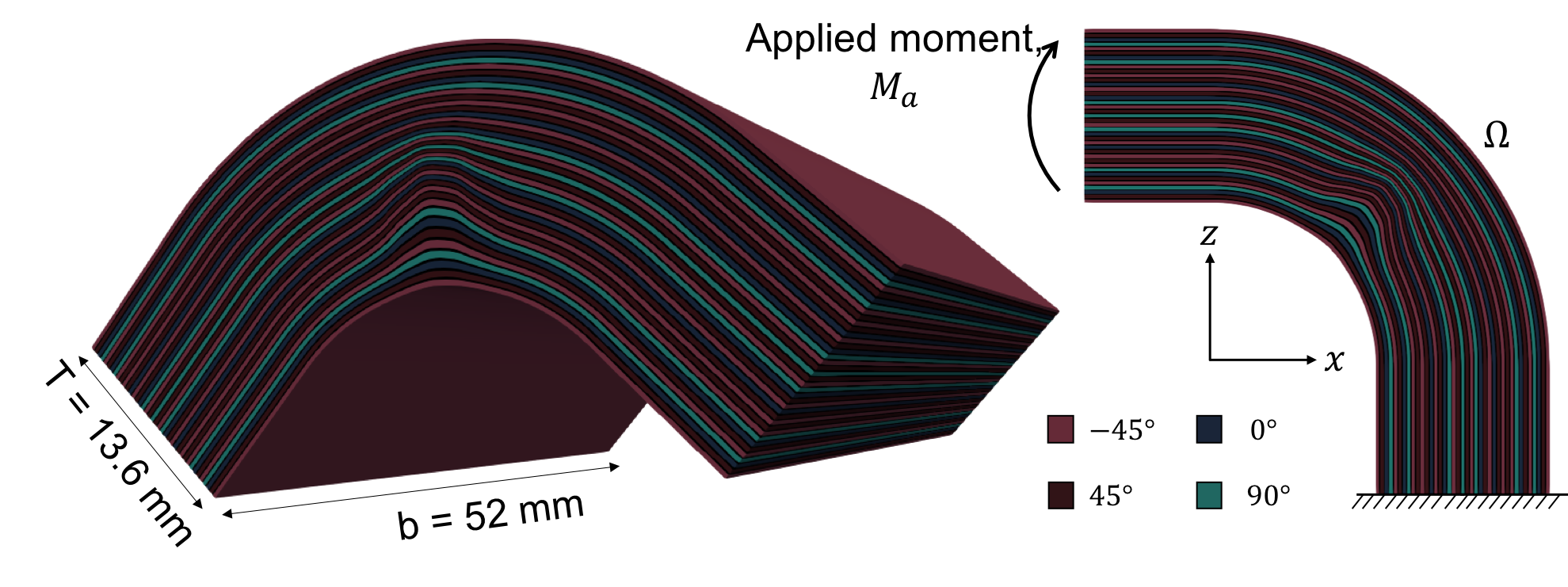
In the simulation the composite strength of a corner part with a wrinkle is modeled and the maximum deflection is returned. The stacking sequence of the composite corner part can be set using the “stack” configuration parameter, by default a 12 layer setup is used. A simplified model for a 3D bending test was used. The curved composite parts were modelled with shortened limbs of length 10 mm. A unit moment was applied to the end of one limb using a multi-point constraint, with homogeneous Dirichlet conditions applied at the end of the opposite limb. This gives the same stress field towards the apex of the curved section as a full 3D bending test. The analysis assumes standard anisotropic 3D linear elasticity and further details on the numerical model and discretisation can be found in [1].

The wrinkle defect is defined by a deformation field \(W:\Omega \rightarrow \mathbb R^3\) mapping a composite component from a pristine state to the defected state.

The wrinkles are defined by the wrinkle functions

\[ W(x,\xi) = g_1(x_1)g_3(x_3)\sum_{i=1}^{N_w} a_i f_i(x_1,\lambda), \]

where \(g_i(x_i)\) are decay functions , \(f_i(x_1,\lambda)\) are the first \(N_w\) Karhunen-Lo’{e}ve (KL) modes parameterized by the length scale \(\lambda\) and \(a_i\) the amplitudes. The amplitude modes and the length scale can be taken as random variables, so that the stochastic vector is defined by \(\boldsymbol \xi = [a_1,a_2,\ldots,a_{N_w},\lambda]^T\). The wrinkles are prismatic in \(x_2\), e.g. the wrinkle function is assumed to have no \(x_2\) dependency. For more details on the wrinkle representation see [2].

References

• [1] Anne Reinarz, Tim Dodwell, Tim Fletcher, Linus Seelinger, Richard Butler, Robert Scheichl, Dune-composites – A new framework for high-performance finite element modelling of laminates, Composite Structures, 2018.

• [2] Anhad Sandhu and Anne Reinarz and Tim Dodwell, A Bayesian framework for assessing the strength distribution of composite structures with random defects, Composite Structures, 2018.