Analytic Banana

Overview

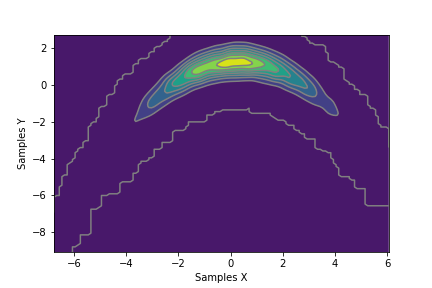
This benchmark consists of an analytically defined PDF \(\pi : \mathbb{R}^2 \rightarrow \mathbb{R}\) resembling the shape of a banana. It is based on a transformed normal distribution. The variance may be adjusted.

Authors

• Linus Seelinger

Run

docker run -it -p 4243:4243 linusseelinger/benchmark-analytic-banana

Properties

Model	Description
posterior	Posterior density

posterior

Mapping	Dimensions	Description
input	[2]	2D coordinates \(x \in \mathbb{R}^2\)
output	[1]	Log PDF \(\pi\) evaluated at \(x\)

Feature	Supported
Evaluate	True
Gradient	False
ApplyJacobian	False
ApplyHessian	False

Config	Type	Default	Description
a	double	2.0	Transformation parameter
b	double	0.2	Transformation parameter
scale	double	1.0	Scaling factor applied to the underlying normal distribution’s variance

Mount directories

Mount directory	Purpose
None

Source code

Model sources here.

Description

We begin with a normally distributed random variable \(Z \sim \mathcal{N}(\begin{pmatrix} 0 \\ 4 \end{pmatrix}, scale \begin{pmatrix} 1.0 & 0.5\\ 0.5 & 1.0 \end{pmatrix})\), and denote its PDF by \(f_Z\).

In order to reshape the normal distribution, define a transformation \(T : \mathbb{R}^2 \rightarrow \mathbb{R}^2\)

\[\begin{split} T(x) := \begin{pmatrix} x_1 / a \\ a x_2 + a b (x_1^2 + a^2) \end{pmatrix}. \end{split}\]

Finally, the benchmark log PDF is defined as

\[ log(\pi(x)) := log(f_Z(T(x))). \]

This distribution is inspired by Chi Feng’s excellent online mcmc-demo.