L2-Sea hull optimization

Overview

This optimization benchmark is based on the L2-Sea model. The goal is to optimize the ship hull’s shape to minimize total resistance.

Authors

• Andrea Serani

• Matteo Diez

Run

docker run -it -p 4242:4242 linusseelinger/model-l2-sea

Properties

Model	Description
forward	l2-sea

forward

Mapping	Dimensions	Description
input	[14]	The 14 inputs are the \(x\) design variables for the shape modification with \(-1\leq x_i \leq 1\) (with parent hull has \(x_i = 0\)) for \(i=1,\dots,14\).
output	[5]	The first output is the model scale total resistance (\(R_\mathrm{T}\)) in Newton, whereas the other four are geometrical constraints (negative to be satisfied), related to the beam, draft, and sonar dome dimensions.

Feature	Supported
Evaluate	True
Gradient	False
ApplyJacobian	False
ApplyHessian	False

Config	Type	Default	Description
fidelity	integer	7	Fidelity level for the total resistance evaluation associated to the numerical grid discretization. Fidelity goes from 1 to 7, where 1 is highest-fidelity level (finest grid) and 7 is the lowest-fidelity level (coarsest grid).

Mount directories

Mount directory	Purpose
/output	ASCII files for visualization of pressure distribution along the hull preXXXX.plt and free-surface intfrXXXX.plt formatted for Tecplot and Paraview, where XXXX is the Froude number.

Source code

Model sources here.

Description

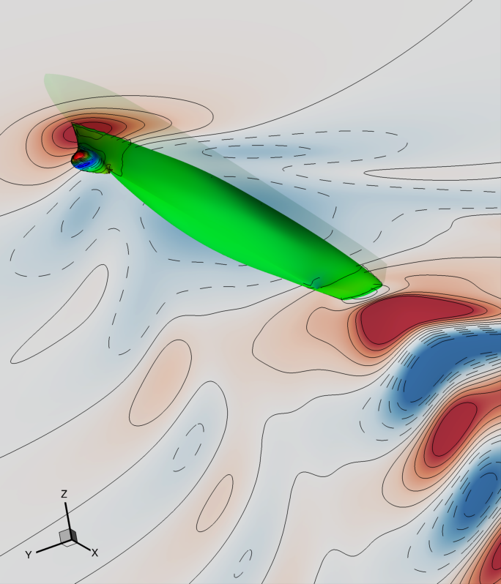
The benchmark, developed within the activities of the NATO-AVT-331 Research Task Group on ‘’Goal-driven, multifidelity approaches for military vehicle system-level design’’ Beran et al. (2020), pertains to the total resistance reduction of the DTMB 5415 in calm water at fixed speed, corresponding to a Froude number (Fr) equal to 0.28. The optimization problem reads

(1)\[\begin{eqnarray}\label{eq:5415prob} \begin{array}{rll} \mathrm{minimize} & \Delta R (\mathbf{x}) = \frac{R (\mathbf{x})}{R_0}-1 \qquad \mathrm{with} \qquad \mathbf{x}\in\mathbb{R}^N\\ \mathrm{subject \, to}& L_{\rm pp}(\mathbf{x}) = L_{\rm pp_0}\\ \mathrm{and \, to} & \nabla(\mathbf{x}) = \nabla_0 \\ & |\Delta B(\mathbf{x})| \leq 0.05B_0 \\ & |\Delta T(\mathbf{x})| \leq 0.05T_0 \\ & V(\mathbf{x})\geq V_0\\ & -1\leq x_i \leq 1 \qquad \mathrm{with} \qquad \forall i=1,\dots, N\\ \end{array} \end{eqnarray}\]

where \(\mathbf{x}\) are the design variables, \(L_{\rm pp}\) is the length between perpendiculars, \(B\) is the overall beam, \(T\) is the drought, and \(V\) is the volume reserved for the sonar in the bow dome. Subscript ‘’0’’ indicates parent (original) hull values. Equality and inequality constraints for the geometry deformations are taken from Grigoropoulos et al. (2017).

The shape modifications \(\tilde{\boldsymbol{\gamma}}(\boldsymbol{\xi},\mathbf{x})\) are produced directly on the Cartesian coordinates \(\boldsymbol{\xi}\) of the computational body surface grid \(\mathbf{g}\), as per

(2)\[\begin{equation}\label{eq:reducedspace} \mathbf{g}(\boldsymbol{\xi},\mathbf{x})=\mathbf{g}_0(\boldsymbol{\xi}) + \boldsymbol{\gamma}(\boldsymbol{\xi},\mathbf{x}) \end{equation}\]

where \(\mathbf{g}_0\) is the original geometry and \(\boldsymbol{\gamma}\) is a shape modification vector obtained by a physics-informed design-space dimensionality reduction Serani et al. (2019)

(3)\[\begin{equation} {\boldsymbol{\gamma}}(\boldsymbol{\xi},\mathbf{x}) = \sum_{k=1}^N x_k \boldsymbol{\psi}_k(\boldsymbol{\xi}) \label{e:exp_gamma} \end{equation}\]

with \(\boldsymbol{\psi}\) a set of orthonormal functions, with \(N=14\) the number of design variables (\(\mathbf{x}\)). It may be noted that the design variables and the associated shape modifications are organized in a hierarchical order, meaning that the first variables produce larger design modifications than the last ones Serani et al. (2021).

The multifidelity levels are defined by the computational grid size. Specifically, the benchmark is defined with seven grid (fidelity) levels with a refinement ratio of 2\(^{0.25}\)