Boundary condition inversion in a three-dimensional 𝑝-Poisson nonlinear PDE¶

Overview¶

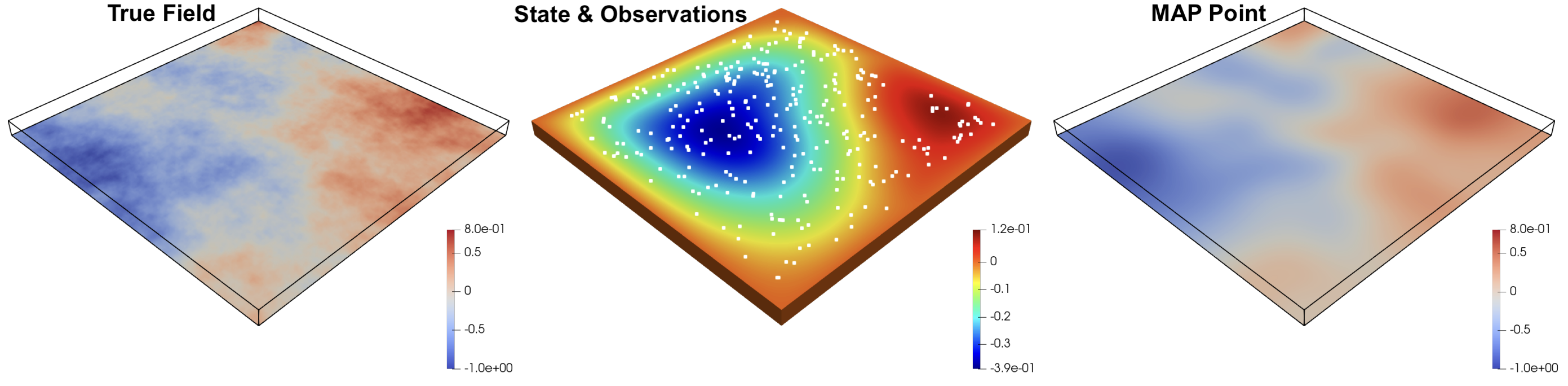
This is an implementation of the 3D nonlinear Bayesian inverse problem described in Section 5.2 of [Kim et al., 2021]. The inverse problem estimates a two dimensional flux boundary condition on the bottom of a three dimensional domain with nonlinear p-Poisson PDE. Observations of the PDE solution at the top of the domain are used.

Domain

The parameter and PDE state parameter are discretized with linear finite elements on a regular tetrahedral mesh. Efficient derivative information is available through the adjoint techniques implemented in hIPPYlib and hippylib2muq.

Authors¶

Run¶

docker run -it -p 4243:4243 linusseelinger/benchmark-p-poisson:latest

Properties¶

Model	Description
posterior	Posterior density

posterior¶

Mapping	Dimensions	Description
input	[233289]	The value of \(m(x)\) at each node in the finite element discretization.
output	[1]	The log posterior density.

Feature	Supported
Evaluate	True
Gradient	True
ApplyJacobian	True
ApplyHessian	True

Config	Type	Default	Description
None

Mount directories¶

Mount directory	Purpose
None

Source code¶

Model sources here.

Description¶

This benchmark defines a Bayesian posterior density over a spatially boundary condition \(m(x)\) given noisy observations of the solution of the nonlinear partial differential equation

\[\begin{split} \begin{aligned} -\nabla\cdot\left[|\nabla u|_\epsilon^{p-2} \nabla u\right] &= f & \text{ on } \Omega \\ u & = g & \text{ on } \partial\Omega_D \\ |\nabla u|_\epsilon^{p-2} \nabla u \cdot \hat{n} & = m & \text{ on } \partial\Omega_N \end{aligned} \end{split}\]

where \(\Omega\) is the computational domain, \(u(x)\) is the solution and\(g\) are prescribed Dirichlet conditions on the boundary \(\Omega_D\subseteq \partial \Omega\). In this benchmark we set \(p=3\) and \(f=0\). The domain, illustrated in the figure above, is \(\Omega = [0,1]^2\times [0,0.05]\).

The prior distribution on the boundary condition \(m(x)\) is a Gaussian process defined through a stochastic differential equation. See Section 5.1.2 of [Kim et al., 2021] for specific details.

The likelihood is formed from observations of \(u(x)\) at 300 points \(x^{i}\) drawn uniformly over the top surface of the domain. Gaussian noise with a standard deviation of \(0.005\) is assumed.

The model, prior, likelihood, and posterior are implemented with the hippylib2muq package, which enables efficient calculation of gradients, Jacobian actions, and Hessian actions using adjoint and tangent linear techniques. MCMC results using MUQ with specific details of the implementation can be found in [Kim et al., 2021].