The cookies model

Overview

This model implements the so-called ‘cookies problem’ or ‘cookies in the oven problem’ (see for reference [Bäck et al.,2011], [Ballani et al.,2015], [Kressner et al., 2011]), i.e., a simplified thermal equation in which the conductivity coefficient is uncertain in 8 circular subdomains (‘the cookies’), whereas it is known (and constant) in the remaining of the domain (‘the oven’). The PDE is solved by an isogeometric solver with maximum continuity splines, whose degree can be set by the user. See below for full description.

Authors

• Massimiliano Martinelli

• Lorenzo Tamellini

Run

docker run -it -p 4242:4242 linusseelinger/cookies-problem

Properties

Model	Description
forward	Forward evaluation of the cookies model, all config options can be modified by the user (see below)
benchmark	Sets the config options for the forward UQ benchmark (see benchmark page)

forward

Mapping	Dimensions	Description
input	[8]	These values modify the conductivity coefficient in the 8 cookies, each of them must be greater than -1 (software does not check that input values are valid)
output	[1]	The integral of the solution over the central subdomain (see definition of \(\Psi\) below)

Feature	Supported
Evaluate	True
Gradient	False
ApplyJacobian	False
ApplyHessian	False

Config	Type	Default	Description
NumThreads	integer	1	Number of physical cores to be used by the solver
BasisDegree	integer	4	Default degree of spline basis (must be a positive integer)
Fidelity	integer	2	Controls the number of mesh elements (must be a positive integer, see below for details)

Mount directories

Mount directory	Purpose
None

Source code

Model sources here.

Description

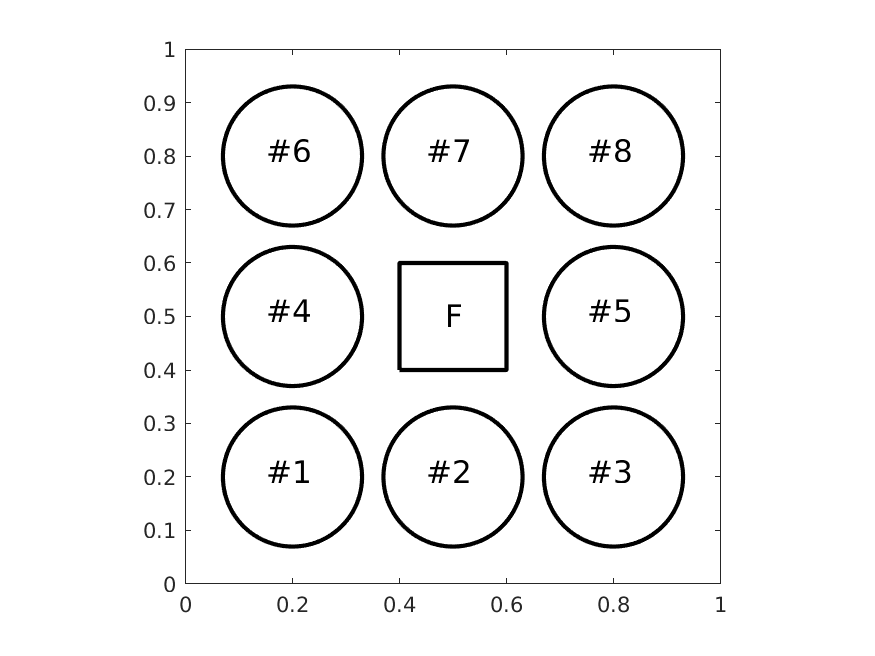
The model implements the version of the cookies problem in [Bäck et al.,2011], see also e.g. [Ballani et al.,2015], [Kressner et al., 2011] for slightly different versions. With reference to the computational domain \(D=[0,1]^2\) in the figure above, the cookies model consists in the thermal diffusion problem below, where \(\mathbf{y}\) are the uncertain parameters discussed in the following and \(\mathrm{x}\) are physical coordinates

\[-\mathrm{div}\Big[ a(\mathbf{x},\mathbf{y}) \nabla u(\mathbf{x},\mathbf{y}) \Big] = f(\mathrm{x}), \quad \mathbf{x}\in D\]

with homogeneous Dirichlet boundary conditions and forcing term defined as

\[\begin{split}f(\mathrm{x}) = \begin{cases} 100 &\text{if } \, \mathrm{x} \in F \\ 0 &\text{otherwise} \end{cases}\end{split}\]

where \(F\) is the square \([0.4, 0.6]^2\). The 8 subdomains with uncertain diffusion coefficient (the cookies) are circles with radius 0.13 and the following center coordinates:

cookie	1	2	3	4	5	6	7	8
x	0.2	0.5	0.8	0.2	0.8	0.2	0.5	0.8
y	0.2	0.2	0.2	0.5	0.5	0.8	0.8	0.8

The uncertain diffusion coefficient is defined as

\[a = 1 + \sum_{i=1}^8 y_n \chi_n(\mathrm{x})\]

where \(y_n>-1\) and

\[\begin{split}\chi_n(\mathrm{x}) = \begin{cases} 1 &\text{inside the n-th cookie} \\ 0 &\text{otherwise} \end{cases}\end{split}\]

The output of the simulation is the integral of the solution over \(F\), i.e. \(\Psi = \int_F u(\mathrm{x}) d \mathrm{x}\)

The PDE is solved with an IGA solver (see e.g. [Da Vaiga et al., 2014]) that uses as basis splines of degree \(p\) (tunable by the user, default \(p=4\)) of maximal regularity, i.e. of continuity \(p-1\). The computational mesh is an \(N\times N\) quadrilateral mesh (cartesian product of knot lines) with square elements, with \(N=100 \times \mathrm{Fidelity}\). The implementation is done using the C++ library IGATools [Pauletti et al., 2015], available at gitlab.com/max.martinelli/igatools.